The Syracuse (or Collatz) conjecture
Specification
The problem is the following one, consider the function :
| let n be a natural integer, f(n)= |
| n/2 |
if n is even |
| 3n+1 |
if n is odd |
|
Then iterates this function until you reach 1 (f(f(...f(n)...))
= 1). The conjecture asserts 1 is reached after a finite number of iterations
for every
n>0.
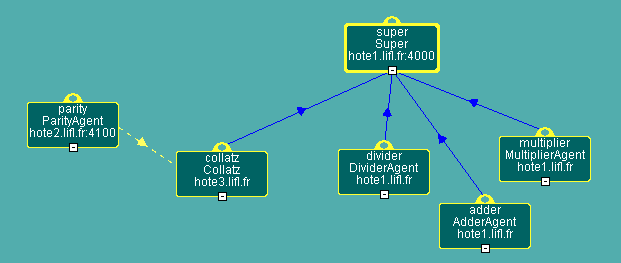
The involved agents of the solution
To solve this problem, we define several (very) specialized agents :
-
one is able to test the parity of an integer, with the isEven
function ;
-
one to manage the conjecture : from n it iterates the collatz function
until 1 is reached, for doing that this agents has no computing skills,
then he must delegate calculus...
-
one can perform quotients of two naturals, with the quotient function
;
-
one can perform additions of two naturals, with the add function
;
-
one can perform multiplications of two naturals, with the mult
function ;
And we add a supervisor with the four last above agents belonging to its
team. The supervisor does nothing else than being the links between other
agents and he manages requests routing.
The parity agent is directly connected to the collatz agent, with no
hierarchical relationship (just to show it is possible).
Supervisor, adder, divider and multiplier are seated in the same JVM
on a given host, collatz and parity agent are distributed over two other
machines.
The structure (the agents and their methods) is then :
|
Super
|
|
Collatz
xByTwo
testParity
threeTimesPlus1 |
ParityAgent
isEven |
AddingAgent
add |
DividerAgent
quotient |
MultAgent
mult |
|
Comments
- 2 versions are proposed : one creates different agent classes,
the second uses skills dynamic acquisition from basic Agent class
instances. This second solution corresponds more to the Magique
programming "philisophy" we want to developp.
-
the MultiplierAgent is exactly
the same as in the factorial solution : agents
can be reused in different contexts
