
Exercice 1
Un processeur à 40 MHz exécute
un programme de benchmark qui utilise un mélange de 4 types d'instruction:
| Type instruction | Nombre d'instruction | Nombre de cycle |
| Integer | 45000 | 1 |
| Transfert de données | 32000 | 2 |
| Floating point | 15000 | 2 |
| Contrôle | 8000 | 2 |
Déterminez le nombre de cycle moyen par instruction, le nombre d'instruction par seconde moyen et le temps d'exécution du programme.
Exercice 2
Le programme suivant, composé de 6 instructions, doit être exécuté 64 fois pour évaluer l'expression arithmétique : D(I) = A(I) + B(I) x C(I) avec IÎ[0..63]
Load R1, B(I) /R1 ¬ Mem (b + I )/
Load R2, C(I) /R2 ¬ Mem (c + I)/
Mult R1, R2 /R1 ¬ (R1) x (R2)/
Load R3, A(I) /R3 ¬ Mem (a + I)/
Add R3, R1 /R3 ¬ (R3) + (R1)/
Store D(I), R3 /Mem (d + I) ¬ (R3)/
R1, R2 et R3 sont des registres du CPU, (Ri) le contenu du registre Ri, a, b, c, d sont les adresses respectives de A, B, C, D. On suppose que le Load/Store prend 4 cycles, le Add 2 cycles et le Mult 8 cycles.
1) Calculez le nombre total de cycles CPU pour exécuter le code sur un processeur SISD.
2) On considère une machine SIMD composée de 64 processeurs qui fonctionnent de manière synchrone. Calculez le temps d'exécution du programme sur cette machine.
5)Même question avec IÎ[0..31]
6)Même question avec IÎ[0..99]
Exercice 3
Le programme Fortran suivant est exécuté sur un monoprocesseur. La version parallèle est exécutée sur un multiprocesseur à mémoire partagée.
L1: Do 10 I = 1, 1024
L2: SUM(I) = 0
L3: Do 20 J = 1, I
L4: 20 SUM(I) = SUM(I) + I
L5: 10 Continue
On suppose que les instructions 2 et 4 prennent chacune 2 cycles machine, y compris CPU et accès mémoire. On ignore le coût causé par le contrôle de la boucle (instructions 1,3 et 5) ainsi que les surcoûts du système lui-même.
1) Quel est le temps d'exécution du programme sur le monoprocesseur?
2) On partage l'exécution de la boucle sur 32 processeurs de la façon suivante: le processeur 1 exécute les 32 premières itérations, le processeur 2 les itérations 33 à 64 etc...Quel est le temps d'exécution et le facteur d'accélération par rapport au monoprocesseur?
On désire calculer en parallèle la somme des quatre éléments du produit de deux matrices A, B 2x2. L'algorithme se compose donc de deux phases: le produit de matrice C = AxB puis la somme des quatre éléments de C. Pour réaliser ce programme il faut 8 multiplications et 7 additions.
1) Construisez le graphe du programme parallèle.
2) Sachant qu'une multiplication prend 101 cycles, une addition 8 cycles et une communication entre deux processeurs 212 cycles, donnez les temps d'exécution en séquentiel et en parallèle sur 8 processeurs. On pourra à l'aide d'un dessin représenter dans le temps le déroulement du programme. Quel est le speedup obtenu?
Sur 2 processeurs ?
Comment obtenir la somme sur tous les processeurs ?
On utilise une machine SIMD de 64 Processeurs Elémentaires (PE) à
mémoire distribuée. Chaque processeur possède les registres A,B,C,D,I,R.
une unité de contrôle (ACU) pilote l'ensemble des PE. Et dispose de ses propres registres INX1, INX2, INX3, INX4, INX5. Les PE sont reliés par un réseau de communication.
On dispose des instructions suivantes
Instruction ACU :
MVI INXi ,# move immédiat dans INXi
INC INXi incrément de INXi : INXi <= INXi + 1
JLT INXi, INXj, Label Branchement conditionnel si INXi<INXj goto Label
LT less than GT greater than etc...
Instruction SIMD :
VLOAD r Adressage indirect indexé : r <= ( (Di) + (Ii))
(3cycles) r Î {Ai,Bi,Ci,Ri}
VMOV r1, r2 Transfert registres r1 <= (r2)
(1cycle) r1,r2 Î {Ai,Bi,Ci,Di,Ii,Ri}
VMVI r,# move immédiat r <= #
(2cycles) r Î {Ai,Bi,Ci,Di,Ii,Ri}
VSTORE r Adressage indirect indexé : (Di) + (Ii) <= (r )
(3cycles) r Î {Ai,Bi,Ci,Ri}
VADD r1, r2 Addition registres r1 <= (r1) + (r2)
(2cycles) r1,r2 Î {Ai,Bi,Ci,Di,Ii,Ri}
VADDI r,# Addition immédiat r <= (r ) + #
(3cycles) r Î {Ai,Bi,Ci,Di,Ii,Ri}
LCYCLE r left cyclic Ri-s <= (Ri) avec s = 2d et d = (r )
(3cycles)
Soit trois vecteurs A, B, C rangé dans les mémoires locales de chaque PE.
Donner les codes assembleur des boucles suivantes en ayant précisé le rangement initial de A, B et C.
For I = 0 to 639 A(I) = B(I) + C(I) dimension de A, B et C de 640 éléments
For I = 0 to 31 A(I) = B(I) + C(I) dimension de A, B et C de 64 éléments
For I = 0 to 630 A(I) = B(I) + C(I) dimension de A, B et C de 640 éléments
For I = 0 to 63 S = S + A(I) dimension de A de 64 éléments
For I = 0 to 63 For J = 0 to I A(I) = A(I) + B(J) dimension de A, B de 64 éléments
Exercice 1
Dans le réseau de Bénes
1) Donnez tous les chemins possibles entre l'entrée 1 et la sortie 1
2) Donnez une configuration permettant les connections simultanées (1,0), (2,2), (4,6) et (7,4)
Exercice 2
Nous allons nous intéresser aux algorithmes de tri et de fusion parallèles: Algorithmes de Batcher.
La fusion de 2 listes triées X et Y permet d'obtenir une liste résultat triée Z telle que chaque élément zi de Z appartienne à X ou Y et que chaque xi et yi apparaissent exactement une fois dans Z.
On dispose d'un comparateur élémentaire 2 entrées et 2 sorties.

Proposer un réseau qui fusionne 2 listes triées de 4 éléments
4) Proposer une méthode de
construction itérative pour un réseau triant des listes de
2n éléments. Quel est le nombre de comparateur total et le
nombre de comparateur à traverser pour un des éléments
de la liste X ou Y.
Exercice 3
On dispose d'un commutateur 2 entrées, 2 sorties. Dans l'état de commande 0 ( resp 1) les lignes sont reliées directement (resp en se croisant).
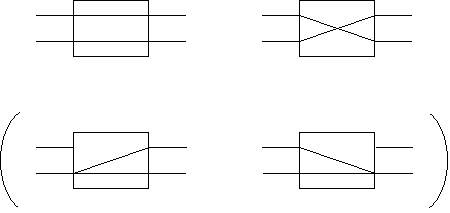
Etat 0 Etat 1
L'exercice consiste à réaliser un crossbar à partir de ce commutateur élémentaire.
1) Construisez un crossbar 2x3 avec 6 commutateurs, en utilisant les commutateurs comme connecteurs.
2) Construisez un crossbar N x P
et précisez les commandes de chaque commutateur ij pour établir
une liaison entre une entrée p et une sortie m 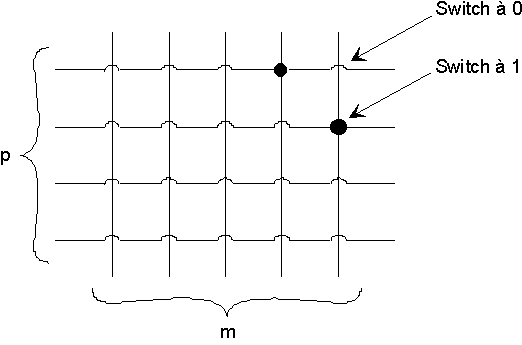
Exercice 4
L'ensemble de l'exercice concerne les communications entre processeurs, plus particulièrement la communication en échange total sur une machine de P processeurs: chaque processeur doit communiquer son propre message à tous les autres (chacun se retrouve avec P messages).
Nous considérons ici que tous les processeurs exécutent le même algorithme. On pourra définir l'algorithme en un seul processeur.
Partie 1
On considère des réseaux de communications statiques où les communications se font par envoi de messages ( procédure envoyer et recevoir ) sur des liens. Un seul message à un instant donné peut circuler dans chaque sens sur un lien bidirectionnel reliant deux processeurs.
1) Proposer un algorithme d'échange total sur un réseau en anneau
a - qui fait circuler les messages toujours dans le même sens
b - qui utilise les deux directions droite et gauche.
On dispose des procédures envoyer à droite, à gauche et recevoir de droite, de gauche. Dans les deux cas combien de phases de communication sont nécessaires?
2) Proposer un algorithme d'échange total sur une grille 2D torique (P= p2 processeurs). On dispose des procédures envoyer au Nord Sud Est et Ouest ( idem pour recevoir ). Combien de phases de communication sont nécessaires?
3) Proposer un algorithme d'échange total sur un hypercube de dimension 3, puis de dimension N. Combien de phases de communication sont nécessaires?
Partie 2
On considère un réseau de communication dynamique non bloquant (ex: Bénes). A chaque phase de communication un processeur peut établir une communication avec un autre processeur si les deux sont libres.
1) Proposez une méthode d'échange total où chaque processeur envoie successivement son message aux autres processeurs. Donnez le nombre de phases de communication. Explicitez cette solution pour 8 processeurs.
2) Proposez une solution où
chaque processeur envoie son message à un seul processeur. Celui-ci
transmet ensuite le message vers un autre processeur etc... jusqu'à
l'échange total. Donnez le nombre de phases de communication. Explicitez
cette solution pour 8 processeurs.
Exercice 5
On suppose une architecture de N processeurs reliés par B bus (N>>B).
On appelle bus à recouvrement le réseau d'interconnexion à base de bus multiples suivant. Chaque bus n'est accessible que par un nombre limité de processeurs. Le réseau est construit suivant le schéma de la fig.1. Sur un bus, on ne peut assurer qu'une communication entre un couple de processeurs. Les bus sont rebouclés en anneau, les valeurs de N et B sont choisies pour permettre cette construction en anneau.
1) On appelle décalage local de taille D, l'opération de communication où chaque processeur doit émettre vers la mémoire du noeud situé à une distance D sur l'anneau (vers la droite si positif). Proposer un algorithme de routage pour réaliser cette opération. Donner le nombre de phases de transfert sur le bus nécessaire en fonction de D, B, N.
2) On appelle diffusion, l'opération de communication qui consiste à envoyer la même donnée depuis un processeur vers tous les autres. Proposer un algorithme de routage. Donner le nombre de phases de transfert sur le bus nécessaire en fonction de B, N.

Mémoires
Exercice 1
Un processeur adresse une mémoire de 232mots. On désire utiliser une mémoire cache de 16 Kmots de capacité. Les mots sont de 32 bits. Pour chaque construction donnez le nombre de champs de l'adresse et la taille de chacun, puis calculez la taille totale du cache en bits ( TAG + data + ... )
a) En direct mapping
b) En direct mapping par bloc de 16 mots
c) En Full associative
En set-associative par ensemble de 16 blocs de 8 mots
Un programme se compose de deux boucles FOR imbriquées, une petite boucle interne et une plus grande externe. La structure générale du programme est la suivante:
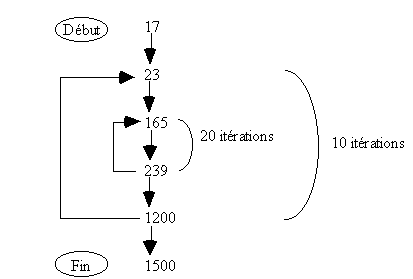
Les adresses mémoires décimales données déterminent l'emplacement des deux boucles ainsi que le début et fin du programme. Tous les emplacements mémoire contiennent des instructions devant être exécutées séquentiellement. Le programme s'exécute sur un processeur avec cache mémoire. Le cache est organisé en direct mapping. La mémoire est de 64K mots, le cache est de 1K mots , il est organisé en bloc de 128 mots.
a)Précisez les différents champs d'une adresse ainsi que leur taille.
b)En ne tenant compte que de l'accès mémoire pour le chargement d'une instruction, donnez le temps de chargement moyen d'une instruction de ce programme. On pose M le temps d'accès à la mémoire d'un bloc et m le temps d'accès au cache d'une instruction
Exercice 3
Lors d'une exécution d'un programme, on observe la trace des pages suivantes : P = r1, r2, r3, ........ rk, rk+1, ..... où rk est le numéro de la page qui contient la kième référence du programme.
Exemple
trace a b c b
défaut * * *
cache a a c c
1)Donner le contenu de la mémoire cache, la présence de défaut de cache pour chaque référence. La mémoire cache contient 2 pages.
Pour un algorithme de remplacement LRU
Est-on loin de l'optimal ?
3)LRU et FIFO semblent de " bons
" algorithmes. L'algorithme MRU Most Recently Used semble intuitivement
mauvais. Comparer avec les résultats précédents. Peut-on
juger de l'efficacité d'un algorithme sur une seule trace de programme
?
Exercice 4
Ce problème consiste à distribuer une structure de données sur une machine pipe-line vectorielle à mémoire entrelacée. Soit Mat une matrice 8x8.
La mémoire entrelacée est composée de huit bancs indépendants (accès en parallèle). Chaque banc a un temps de lecture de d cycles processeur.
Proposer un rangement unique permettant le même temps d'accès (le meilleur) pour une ligne et une colonne. Quel est le temps d'accès à la diagonale?
Que se passe-t-il si l'on prend 9 bancs au lieu de 8? Préciser les avantages et inconvénients.
La machine étudiée ressemble fortement aux machines Cray étudiées en cours. Une mémoire est composée de 4 bancs mémoire entrelacés et répartis en 2 lignes de 2 bancs. Chaque banc peut supporter une et une seule requête de lecture ou d'écriture. Une requête (lecture ou écriture) nécessite 4 cycles pour être exécutée. Deux processeurs se partagent cette mémoire. Chaque processeur dispose de 3 ports d'entrée/sortie. Un port d'E/S peut émettre à chaque cycle une requête mémoire. Un Crossbar relie les ports d'E/S avec les lignes de la mémoire partagée.
A chaque cycle une requête par port peut être essayée. Si la mémoire est libre la requête est satisfaite, la requête suivante peut alors être essayée au cycle suivant, sinon la requête non satisfaite devra être réémise au cycle suivant. La traversée du pipe-line d'addition prend également 4 cycles. Le chaînage des ports d'E/S et du pipe-line d'addition est supporté.
On dispose de 3 tableaux A, B, C contenant chacun 4 éléments. La répartition des éléments de A, B et C sur les différents bancs est la suivante:
Banc 2, ligne 1 : A[0] B[2] C[0]
Banc 3, ligne 2 : A[1] B[1] C[3]
Banc 4, ligne 2 : A[2] B[3] C[2]
Représentez par un chronogramme l'activité de chaque banc mémoire lors de la réalisation du code suivant par un seul processeur (déclenchement d'une instruction par cycle)(longueur des vecteurs de 4 éléments)(en cas de conflit priorité sur A puis B puis C):
t : VLOAD A , V0
t+1 : VLOAD B, V1
t+2 : VADD VO, V1, V2
t+3 : VSTORE V2 , C
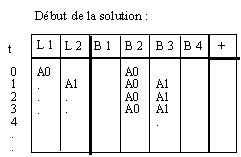
Li requête sur la ligne i
Bi activité du banc i
+ activité du pipeline d'addition
Exercice 6
On dispose de boîtiers mémoire RAM de 8Kmots. Les mots sont de 4 bits.
a) Avec trois boîtiers construisez une mémoire de 16Kmots de 6 bits
b) Avec six boîtiers construisez une mémoire de 32 Kmots de 6 bits.
Il faudra définir précisément la fonction de décodage d'adresse et dessiner les connections aux bus de data, d'adresse et de contrôle.
Pipe-line
Exercice1
Un micro processeur pipe-line possède
5 étages : (IF) Instruction Fetch, (ID) Instruction Decode,(OF)
Operand Fetch , (OE) Operation Execute, (OS) Operand Store. Le tableau
suivant représente les unités utilisées pour certaines
instructions.
| Instruction | T(IF) | T(ID) | T(OF) | T(OE) | T(OS) |
| Load mem/reg | 1 | 1 | 1 | 0 | 0 |
| Load reg/reg | 1 | 1 | 0 | 1 | 0 |
| Store reg/mem | 1 | 1 | 0 | 0 | 1 |
| Add mem/reg | 1 | 1 | 1 | 1 | 0 |
Calculer le temps d'exécution des programmes suivants.
MOV BX ,[200]
MOV CX ,[300]
MOV DX ,[400]
2)
MOV AX ,[100]
MOV BX ,[200]
ADD AX , BX
MOV [200] ,AX ;copie AX vers mémoire 200
Exercice 2
A partir d'un programme en assembleur, on veut exploiter le maximum de parallélisme sur un puis deux processeurs RISC. On suppose qu'il n'y a pas de conflits d'accès aux ressources communes et que le processeur est multi-unités fonctionnelles. Par simplification le processeur n'est pas pipeline et toutes les instructions s'exécutent en 1 cycle machine.
Le programme est le suivant:
1 Load R1 , A /R1 <- Mem(A)/
2 Load R2, B
3 Mul R3, R1, R2 /R3 <- (R1) * (R2)/
4 Load R4, D
5 Mul R5, R1, R4
6 Add R6, R3, R5
7 Store X, R6 /Mem(X) <- (R6)/
8 Load R7, C
9 Mul R8, R7, R4
10 Load R9, E
11 Add R10, R8, R9
12 Store Y, R10
13 Add R11, R6, R10
14 Store U, R11
15 Sub R12, R6, R10
16 Store V, R12
1) Dessinez un graphe qui représente les dépendances de données entre les 16 instructions (les arcs du graphe représentent la réutilisation par une instruction d'un résultat produit par une autre instruction).
2) On considère que le processeur est 3-issues, il peut donc à chaque cycle exécuter 3 instructions: une instruction d'accès mémoire, une instruction Add/Sub et une instruction Mul. Construisez la liste des triplets d'instructions qui seront exécutées à chaque cycle sur ce processeur pour ce programme.
Un monoprocesseur peut fonctionner en scalaire ou en mode vectoriel. En mode vectoriel, les calculs sont exécutés 9 fois plus vite qu'en scalaire. Un programme de benchmark prend T cycle pour s'exécuter sur ce processeur. Une étude du code a montré que 25% du temps T est attribué au mode vectoriel. Pour le reste, le processeur fonctionne en mode scalaire.
1)Calculer le speedup effectif de ce processeur par rapport au même processeur sans mode vectoriel. Donner le pourcentage de code qui a été vectorisé.
2)En supposant que l'on arrive à doubler le ratio des vitesses par des améliorations hardware, que devient le speedup effectif ?
3)En supposant que le même speedup doit être obtenu par une amélioration du compilateur au lieu du hardware. Quelle doit être le pourcentage de code que le compilateur doit vectoriser pour obtenir ce speedup avec le même programme ?
Exercice 4
Ce problème concerne le produit de matrice/vecteur puis matrice/matrice
1) On dispose d'une ligne de processeurs.
Chacun dispose de sa propre mémoire locale, de son propre programme,
de liens de communications avec deux voisins. Chaque processeur possède
deux liens en entrée. Ils sont connectés de la façon
suivante.
On veut réaliser le produit Yi = S j = 1,n Aij Xj. Les éléments du vecteur X sont envoyés successivement en entrée du premier processeur. Les éléments de la première ligne sont envoyés successivement sur le premier processeur, la seconde ligne sur le second etc. Tous les processeurs effectuent le même algorithme:
recevoir des données de la gauche, du haut
calculer
envoyer des données vers la droite
Le résultat Y du produit mat/vect sera réparti sur les différents processeurs. L'idée générale de l'algorithme consiste à se faire rencontrer le couple(Xj, Aij) en même temps sur le processeur i.
a) Définissez le flux d'entrée de chaque processeur (les Aij) en tenant compte des décalages dans le temps. Pour un produit de dimension 4, dessinez les flux de données entre les différentes étapes de calcul. Ex signifie envoyer rien puis c puis rien puis b puis a.
b) Ecrire l'algorithme pour un processeur. Quel est le temps d'exécution total?
2) On veut maintenant calculer un produit matrice/matrice. On dispose pour cela d'une grille 2 dimensions.
Les colonnes de B sont envoyées depuis la gauche, les lignes de A sont envoyées depuis le haut. Là encore il s'agit de réunir les couples (Aik, Bkj) sur le processeur Pij.
a) Précisez les flux d'entrée en haut et à gauche de la grille de processeurs en tenant compte des décalages.
b) Ecrire l'algorithme d'un processeur.
Donnez le temps total de calcul du produit de matrices.
3) A partir du même algorithme, on veut définir un algorithme de produit de matrices sur la MasPar. On utilise le réseau de voisinage Nord, Sud, Est, Ouest qui est torique. Les deux matrices A et B sont ici rangées sur les processeurs.
a) Donnez pour une MasPar de 4x4 PE la répartition initiale de Aij et Bij sur les processeurs Pi'j' pour un produit de matrices 4x4.(sur un dessin)
La mise en oeuvre d'un calcul sur un pipe-line demande plusieurs ressources successives, chacune correspondant à un étage du pipe-line. Plusieurs étages d'un même pipe-line peuvent demander la même ressource et donc entraîner des collisions lors de l'exécution.
Pour éviter ces collisions, on utilise les tables de réservation. Elles permettent de représenter l'état d'occupation des ressources matérielles en fonction des périodes d'horloge. Par exemple pour un additionneur flottant, le premier étage correspond au décalage des mantisses et à la comparaison des exposants (Dénorm), le second est l'addition des mantisses décalées(ALU), le troisième la normalisation des résultats(Norm). La table de réservation comporte trois colonnes.
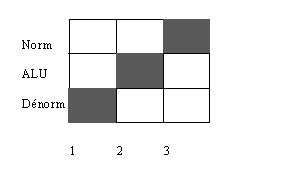
Pour la multiplication, il faut additionner les exposants, multiplier les mantisses ce qui prend 3 cycles (en même temps que l'addition) puis normaliser le résultat.
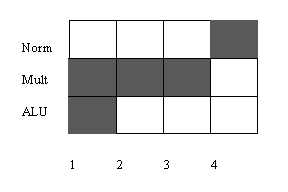
A l'évidence, on peut déclencher une addition à chaque cycle, par contre on ne peut déclencher une multiplication que tous les trois périodes d'horloge.
On désire réaliser un pipe-line qui effectue une multiplication et une addition en série(quand la multiplication est terminée) de type a * x + y. Donnez la table de réservation. Combien de cycles d'attente sont nécessaires entre deux déclenchements (on appelle ce nombre la latence du pipe-line)?
Proposez une autre construction de pipe-line où l'on anticipe le calcul de l'addition (en parallèle avec la multiplication). Que deviennent la table de réservation et la latence ? Comment utiliser ce pipe-line pour calculer a * X + Y ou X et Y sont des vecteurs de n éléments ?
On dispose d'un registre d'état à décalage. Celui-ci doit permettre à chaque top de connaître directement s'il est possible ou non de déclencher un nouveau calcul. Précisez la valeur d'initialisation de ce vecteur d'état lors du lancement du premier calcul, la transformation de ce vecteur à chaque top d'horloge, et la mise à jour de ce vecteur lors du lancement d'un nouveau calcul. Donnez sous forme d'algorithme, le fonctionnement de notre déclencheur de calcul. Décrivez le début de l'algorithme avec le vecteur de collision 1001011 en essayant de lancer un calcul dès que possible.
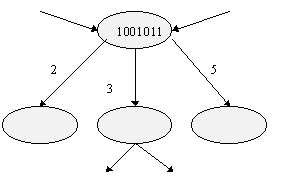
Dessinez le graphe complet pour le vecteur de collision 1001011. Identifiez tous les cycles de ce graphe et montrez que l'un d'entre eux permet d'obtenir le meilleur rendement (nombre de calcul / nombre de top d'horloge). Précisez la technique de calcul du meilleur cycle pour un graphe quelconque.
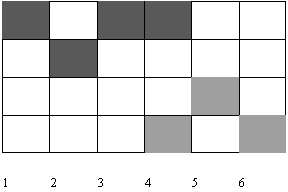
Dessinez le graphe des états et donnez le débit maximum de ce pipe-line. Si l'on suppose qu'il n'y a pas de dépendance entre les gris clair et les gris foncé, proposez une transformation de la table de réservation qui permette d'augmenter le débit maximum. Vérifiez par le nouveau graphe obtenu, la valeur du débit maximum.
Annales
Exercice 1
Une machine massivement parallèle est construite à partir d'un noeud élémentaire appelé PE. Le problème à traiter ne concerne que l'architecture de ce noeud.
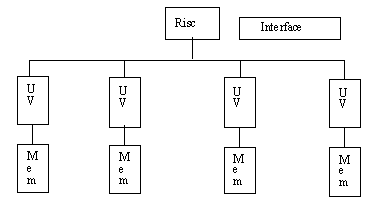
Un noeud est composé d'un
processeur RISC avec sa propre mémoire, de quatre unités
vectorielles, de quatre bancs mémoire, d'un bus interne et d'une
interface réseau. (Fig. 4) Le processeur RISC pilote l'ensemble
du PE. IL exécute le code scalaire et envoie des instructions vectorielles
vers les unités vectorielles : UV. Le fonctionnement de ces UV est
de type SIMD, chaque UV contient un certain nombre de registres V0, V1,
... Vn. Le fonctionnement SIMD impose que tous les UV exécutent
la même instruction sur les même registres. Le format d'adressage
au niveau des instructions de l'UV est soit immédiat, soit direct
registre, soit indirect registre.
Nous ne disposerons que des instructions vectorielles à deux opérandes de la Fig. 5 Vop Source , source/dest. Le code scalaire sera traduit en C standard. Sur le bus interne, un seul transfert à la fois est supporté.
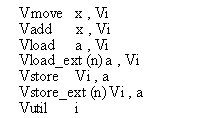
La source a est soit une adresse immédiate, soit un registre Vi pour un adressage indirect- c'est le contenu de chaque registre Vi qui produit l'adresse dans la mémoire locale de l'UV correspondante, soit une variable C - sa valeur sert d'adresse immédiate.
La source i de VUTIL est un immédiat ou un scalaire C, les quatre bits de poids faible sélectionnent les UV qui effectueront l'instruction SIMD - bit 0 -> UV0, etc.(Cf. eflag de la MasPar)
La source n indique le numéro de l'UV où se trouve l'adresse effective a. Cette instruction entraîne une communication sur le bus interne, l'instruction suivante ne pourra être exécutée que lorsque toutes les communications seront effectuées.(au maximum il faut 4 cycles)
On propose de ranger cycliquement les trois vecteurs A B C: A(0) sur UV0, A(1) sur UV1, A(2) sur UV2, A(3) sur UV3, A(4) sur UV0 etc...
1) Décrire l'algorithme en C étendu aux instructions SIMD. Les UV étant des pipelines de 4 étages, donner le nombre de cycle UV nécessaire pour réaliser ce calcul.
2) Décrire l'algorithme pour A ( 10 : 37 : 3) = B ( 20 : 29 ) + C ( 20 : 38 : 2 ) où ( i : j : s ) signifie i = début, j = fin et s = pas ( exemple pour C, on sélectionne 20 22 24 ... ) Existe-t-il un meilleur rangement pour A, B et C? Justifier votre réponse.
3) Décrire l'algorithme pour l'opération S = Sum ( A ) , S étant un tableau de quatre éléments réparti sur les quatre UV, seul S[0] devra contenir la valeur résultat. Sachant qu'une communication sur le bus prend un cycle UV et impose un vidage du pipeline, évaluer le temps de calcul en nombre de cycle UV. Modifier le code pour obtenir le résultat dans les quatre éléments de S.
4) Décrire l'algorithme pour l'opération A ( i ) = ?j=0,i B ( j ) avec iÎ [0 .. 7]
5) On dispose de Crossbar 4 x 4. Proposer une amélioration du noeud, comment le mettre en oeuvre, quels sont les inconvénients?
Avez-vous reconnu la machine à laquelle appartient ce noeud?