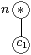Construction d'un automate déterministe à partir d'un arbre de syntaxe abstraite

3 Construction d'un automate déterministe à partir d'un arbre de syntaxe abstraite

3.1 Construction d'ensembles d'états associés à chaque noeud

Pour construire un automate déterministe à partir de cet arbre, il faut calculer pour chaque noeud n les 5 ensembles alphabet(n), initial(n), final(n), suivant(n) et isnul(n) définis à la figure 3.

isnul(n) est une valeur booléenne ;
alphabet(n) est un ensemble de caractères ;
les autres ensembles sont des ensembles d'états de l'automate.

Ces ensembles peuvent se calculer en réalisant un parcours de l'arbre en profondeur d'abord.

Remarques

L'opération ∪ de réunion des ensembles vérifie la relation {i,j} ∪{i,k}={i,j,k}. Les autres opérations sur les ensembles (intersection, complément...) ne sont pas utiles pour ce projet).

Vous êtes libres de choisir votre représentation des ensembles et des états (pour ces derniers, il peut être intéressant de leurs associer une étiquette unique pouvant être en relation avec l'adresse d'un noeud de l'arbre de syntaxe abstraite).

Noeud n initial(n) final(n) isnul(n)

n est une feuille {end} {end} True

étiquetée end (=#)

n est une feuille {i} {i} False

étiquetée i

initial(c₁) ∪ initial(c₂) final(c₁) ∪ final(c₂) isnul(c₁) ou isnul(c₂)

si isnul(c₁) alors

initial(c₁) ∪ initial(c₂)

sinon initial(c₁)

si isnul(c₂) alors

final(c₁) ∪ final(c₂)

sinon final(c₂)
isnul(c₁) and isnul(c₂)

initial(c₁) final(c₁) True

Soit n un noeud de l'arbre,
Construction de l'ensemble suivant :
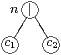
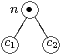
si n est un noeud de concaténation ayant c₁ pour fils droit et c₂ pour fils gauche, et si i appartient à final(c₁), alors tous les éléments de initial(c₂) sont dans suivant(i);
si n est un noeud de répétition, et si i appartient à final(n), alors tous les éléments de initial(n) sont dans suivant(i) ;

Construction de l'ensemble alphabet :
si n est un noeud de concaténation ayant c₁ pour fils droit et c₂ pour fils gauche, alors alphabet(n) est la réunion de alphabet(c₁) et alphabet(c₂) ;
si n est un noeud de répétition, alors alphabet(n) est égal à alphabet(c₁).

Figure 3 : Définition des ensembles alphabet, initial, final, isnul et suivant.

3.2 Construction de l'automate déterministe

Pour obtenir l'automate déterministe à partir de ces ensembles, il reste à appliquer l'algorithme présenté ci-dessous. Cet algorithme construit un ensemble d'états Detat, chaque état représentant un ensemble de noeuds de l'arbre, et une table de transition Dtran, représentant les transitions de l'automate. Ainsi, si Dtran[T, a] = U, alors il y a une transition dans l'automate de l'état T à l'état U étiquetée par la lettre a. Les états de Detat sont marqués pour pouvoir indiquer s'ils ont été examinés ou pas. L'état initial de l'automate est initial(root), les états finaux sont tous les états associé au noeud représentant le symbole de fin.

Algorithme de construction de l'automate déterministe

Initialement, Detat contient un seul état non marqué constitué des éléments de initial(root).
Tant qu'il reste un état T non marqué dans Detat faire

marquer T;
Soit U l'ensemble des noeuds de l'arbre qui sont dans suivant(p), avec p le noeud associé à T.

Pour tout élément de u de U faire :
- Si u qui n'appartient pas déjà à Detat, alors ajouter u à Detat (sans le marquer) ;
- Dtran[T, a] = u pour chaque lettre a dans l'alphabet associé au noeud p.

3.3 Minimisation de l'automate

Veillez à terminer une implantation du filtre mgrep avant d'implanter cette minimisation.

La minimisation d'un automate déterministe M s'effectue en partitionnant l'ensemble de ses états. Le calcul de cette partition Π_finale se fait en appliquant itérativement l'algorithme ci-dessous sur la partition courante Π. Chaque application de cet algorithme à Π calcule une nouvelle partition Π_new, et, lorsque Π_new = Π, on a trouvé la partition finale Π_finale = Π_new. Si Π_new ≢ Π, on réitère l'algorithme en prenant Π = Π_new. Initialement, la partition Π comporte deux groupes, le groupe des états acceptants (finaux), et les états non-acceptants.

Algorithme de partitionnement d'une partition Π

Pour chaque groupe G de Π faire

Partitionner G en sous-groupes, de sorte que
deux états s et t de G sont dans le même sous-groupe si et seulement si, pour toute lettre a de l'alphabet, les états s et t ont une transition par a vers des états qui appartiennent au même groupe de Π;
Remplacer G dans Π_new par l'ensemble des sous-groupes calculés précédemment;

Chaque groupe d'états de Π_finale représente en fait un état de l'automate minimal M'. Pour calculer les transitions de l'automate minimal, on choisit pour chaque groupe de Π_finale un état représentant. Les états de l'automate minimal seront les états représentants. Soit s un état représentant, et supposons qu'il y a une transition par la lettre a dans l'automate non minimal de s vers t. Soit r le représentant du groupe de t, alors on a une transition dans l'automate minimal de s vers r par la lettre a. L'état initial de M' sera le représentant du groupe contenant l'état initial de M, ses états finaux seront les représentants des groupes qui contiennent un état final de M. Il reste à supprimer les états morts (bouclant sur eux-mêmes pour toute lettre) non finaux, et les états non-atteignables depuis l'état initial.