Quatrième semaine

Exercice 1
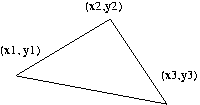
Exercices sur la notion d'héritage : commençons avec la classe Point ! Point.java
Exercice 2
Définition de la classe Polygone ...
 Polygone.java
Exercice 3
Calcul du périmètre d'un polygone.
 Polygone.java
Exercice 4
Définition de la classe Rectangle (un cas particulier de Polygone).
 Rectangle.java
Exercice 5
Définition de la classe Carre (une spécialisation de Rectangle).
 Carre.java
Exercice 6
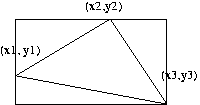
Calcul du Rectangle englobant d'un Polygone.
 Polygone.java

Dans les exercices suivants, vous pourrez supposer que vous disposez de la classe Point :

class Point
{
    protected float x, y;
   
    public Point() { x = 0; y = 0; }

    public Point(float x, float y) { this.x = x; this.y = y;}

    public float getX() { return x; }

    public float getY() { return y; }

    public String toString() { return "("+x+","+y+")";

}


Exercice 1 :

Ajouter à la classe Point une méthode, à résultat réel, renvoyant la distance entre le point courant et le point passé en paramètre.

Rappel : Soient (x1,y1) et (x2,y2) les coordonnées de deux points, alors la distance entre ces deux points est la racinie carrée de (x1-x2)2+(y1-y2) 2.

Rappel : Pour calculer la racine carrée d'un nombre, utilisez la méthode statique double sqrt(double) de la classe Math.



Exercice 2 :

Un polygone peut etre défini par la liste de ses sommets successifs, par exemple un triangle est défini par les coordonnées de ses trois sommets (x1,y1), (x2,y2) et (x3,y3) :

 Image d'un triangle

Ecrire une classe Polygone comportant :
Le nombre de sommets du polygone étant fixé par le nombre d'éléments du tableau de points du constructeur. La méthode d'affichage devra préciser que c'est un polygone.

class TestPolygone
{
    public static void main(String[] args)
    {
        Point[] sommets = new Point[]{new Point(1,1), new Point(1,2), new Point(2,2), new Point(2,1)};
        Polygone p = new Polygone(sommets)

        System.out.println(p);
    }
}
 
Ce programme produira la sortie suivante :
 
C:\Java\Algo> java TestPolygone
Polygone : {(1.0, 1.0) (1.0, 2.0) (2.0, 2.0) (2.0, 1.0)
C:\Java\Algo>


Exercice 3 :

Ajouter à la classe Polygone une méthode, à résultat réel, calculant le périmètre du polygone (somme des cotés).


Exercice 4 :

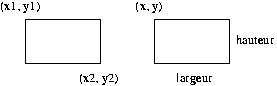
Un rectangle est un polygone particulier (on ne s'intéressera ici qu'aux rectangles ayant leur cotés parallèles aux axes). Plutot que de définir un rectangle par ses quatre sommets, on préfére le définir par deux points opposés ou par un point plus la largeur et la hauteur :

 Illustration des rectangles

Ecrire une classe Rectangle, héritant de la classe Polygone; deux constructeurs seront fournis, l'un avec deux points, l'autre avec un point ete deux réels (largeur et hauteur). La méthode d'affichage précisera que c'est un rectangle. On devra pouvoir utiliser la méthode donnant le nombre de sommets et la méthode calculant le périmètre.

Note : On ne fournira que ce qui est nécessaire, compte tenu de ce qui est apporté par l'héritage !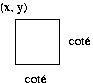


Exercice 5 :

Un carré est un rectangle particulier avec la hauteur qui est égale à la largeur. Un carré peut etre défini par un point plus la longueur de son coté :

 Carre

Ecrire une classe Carre, héritant de la classe Rectangle; un constructeur avec un point et un réel (le coté) sera fourni. La méthode d'affichage précisera que c'est un carré.

Note :On ne fournira que ce qui est nécessaire, compte tenu de ce qui est apporté par l'héritage !


Exercice 6 :

Un polygone peut etre circonscrit par un rectangle, c'est le plus petit rectangle (à cotés parallèles aux axes) contenant tout le polygone :

 Triangle circonscrit dans un rectangle

Ajouter à la classe Polygone une méthode, à résultat Rectangle, retournant le rectangle circonscrit au polygone courant (il faut rechercher l'abcisse minimale et l'abscisse maximale des points, et la meme chose pour l'ordonnée).


La classe permettant de tester votre travail pourra etre la suivante :

class TestPolygone
{
    public static void main(String[] args)
    {
      Point[] ps = new Point[]{new Point(1,1), new Point(1,2), new Point(2,2), new Point(2,1)};

      Polygone p = new Polygone(ps);
      System.out.println(p);
      System.out.println("Périmètre : "+p.perimetre());     

      Rectangle r = new Rectangle(new Point(0,1), new Point(1,0));
      System.out.println(r);
      System.out.println("Périmètre : "+p.perimetre());     

      Rectangle rr = new Rectangle(new Point(0,1), 1, 1);
      System.out.println(rr);
      System.out.println("Périmètre : "+r.perimetre());     

      Rectangle c = new Carre(new Point(0,1), 1);         
      System.out.println(c);
     }
}