Challenge

Problem description

The subject of this challenge is the Development Assurance Level (DAL) Allocation problem. The Development Assurance Level (DAL) indicates the level of rigor of the development of a software or hardware function of an aircraft. The detailed description of the problem is given here

Deadlines

• July, 17th 2014
  • Start of the challenge.
  • Description of the problem unveiled.
  • First set of instances provided as a multi-objectif Pseudo-Boolean Optimization problem (Boolean variables, OPB format).
  • Manifestation of interest starts.
    
• September, 15th 2014 Second set of instanced provided, together with the original Minimal Cut Sets used to derive them. It is thus possible to model the problem differently.
  Providing the MCS allows strictly more freedom than using a constraints based model in XCSP as initially announced.
• November 14th, 2014 Deadline for submitting solvers.
  
• December 15th, 2014 Deadline for submitting the description of the algorithm. Individual results available to participants for self-checking.
  
• January 16th, 2015 Announcement of final result at the LION 9 conference in Lille.
  

Guidelines and Rules

Benchmarks

The benchmarks are provided as a multi-objectif Pseudo-Boolean Optimization problem, that is, modeled with Boolean variables. This is the original modelisation of the problem given in [1]. The original data of the problem are also provided for those willing to try another modelisation or taking advantage of a more expressive language.

A first set of "easy" instances are provided with the benchmarks description to allow participants to test and tune their algorithm.

A second set of "harder" instances are provided with the original data and parameters used to generate them. Such set should allow participants to see how their approach scales on those benchmarks, and to use their own modelisation of the DAL allocation problem.

An additional challenging set of instances will be used to compare the algorithms submitted by each team. Those benchmarks will be made available to the participants after the deadline for submitting solvers.

The easy benchmarks can be solved by the solver Sat4j. To run it, just type : java -jar sat4j-pb.jar file.opb

Evaluation of the solvers

Complete solvers will be evaluated on their ability to solve the benchmarks (number of benchmarks solved) and the time spent to solve those benchmarks (total runtime for the benchmarks solved). The first criteria should be maximized and the second one minimized.

Solvers able to provide an upper bound of the solution will be evaluated according to the quality of the solution found and the time needed to find that solution. For each benchmark, all solvers will be ranked first according to the quality of their solution, then according to the time needed to provide that solution. Such ranking will provide for each solver s and each benchmark b a rank rank(s,b) between 1 and the total number of participating solvers. The score of a solver for the challenge will be the mean of the rank on the individual benchmarks:

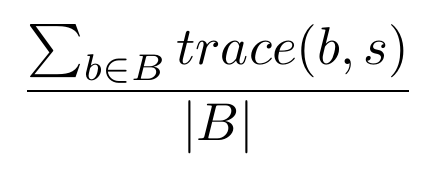
Note that in those rankings, solvers within a one second difference of runtime (or 1% for large runtimes) against the faster solver providing an equaly good solution will be ranked together.

The solvers are expected to be deterministic, i.e. to be able to reproduce their behavior when given a random seed. The solvers will only be launched once on each benchmark, with a timeout of 15 minutes.

[1] Pierre Bieber, Remi Delmas, and Christel Seguin. Dalculus - theory and tool for development assurance level allocation. In Francesco Flammini, Sandro Bologna, and Valeria Vittorini, editors, SAFECOMP, volume 6894 of Lecture Notes in Computer Science, pages 43–56. Springer, 2011.

Output

The solver will have to provide a solution for each of the problem solved. For solvers using the OPB format, the output will the the same of the Pseudo Boolean competition, used by the solver Sat4j.

Organisation

Daniel LE BERRE CRIL, Université d'Artois, France leberre at cril.fr

Olivier ROUSSEL CRIL, Université d'Artois, France roussel at cril.fr

Rémi DELMAS ONERA Toulouse, France Remi.Delmas at onera.fr

Marie-Eléonore MARMION LIFL, Université Lille 1, France marie-eleonore.marmion at lifl.fr